New Math Game Invented at the 2019 National Math Festival
2019 Festival presenter Dr. Jacob M. Ward of American University and the DC Math Circle (opens new window) shared the following guest post with us about a new math game that was created at the 2019 Festival. Try it at home this summer!
We are excited to announce the creation of a new mathematical game at this year’s National Math Festival!
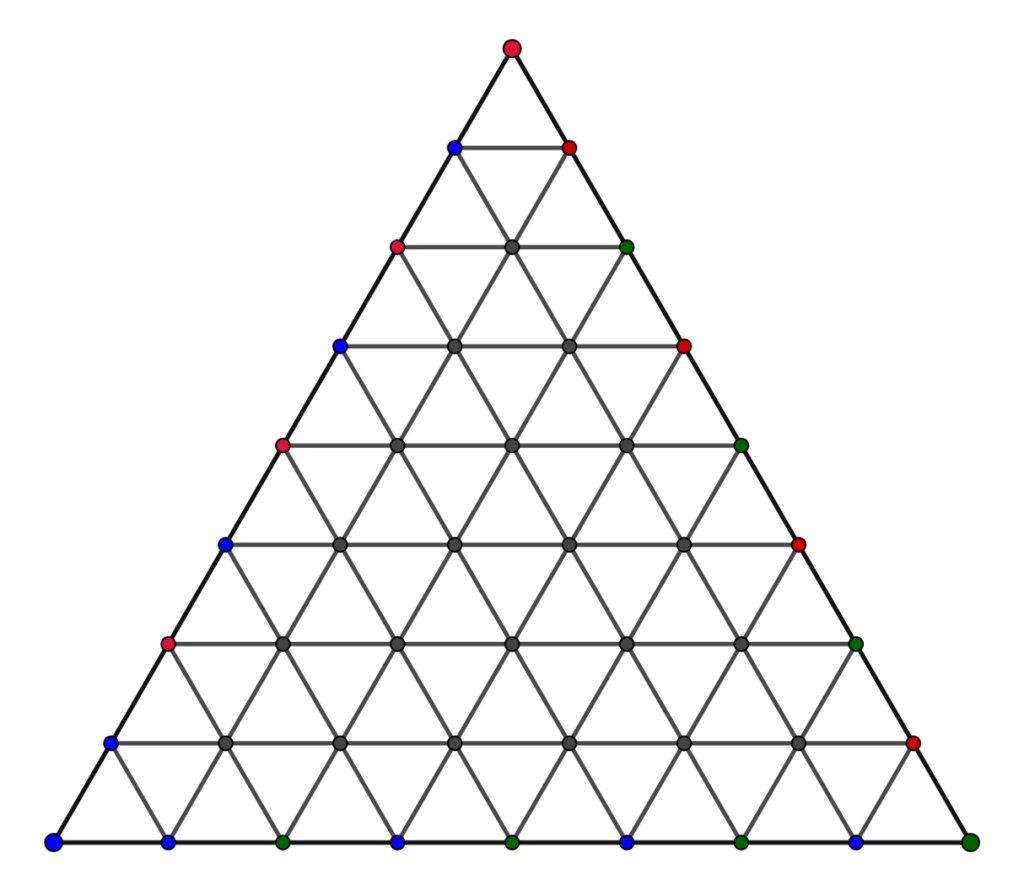
The DC Math Circle (opens new window) featured some well-known games in number and graph theory at the 2019 Festival, including the Four Numbers Game (opens new window), Sprouts (opens new window), and Lights Out (opens new window). Many traditional games, including some of these, have a board on which the game is played, and it’s always desirable that such games carry elegant mathematical features. With this and graph theory in mind from gaming with our inquisitive visitors during the first half of the Festival, I created the game of Tri-umph, or simply Triumph. The board is what mathematicians call a simplex, pictured below, and three colors are used – let’s say red, green, and blue.
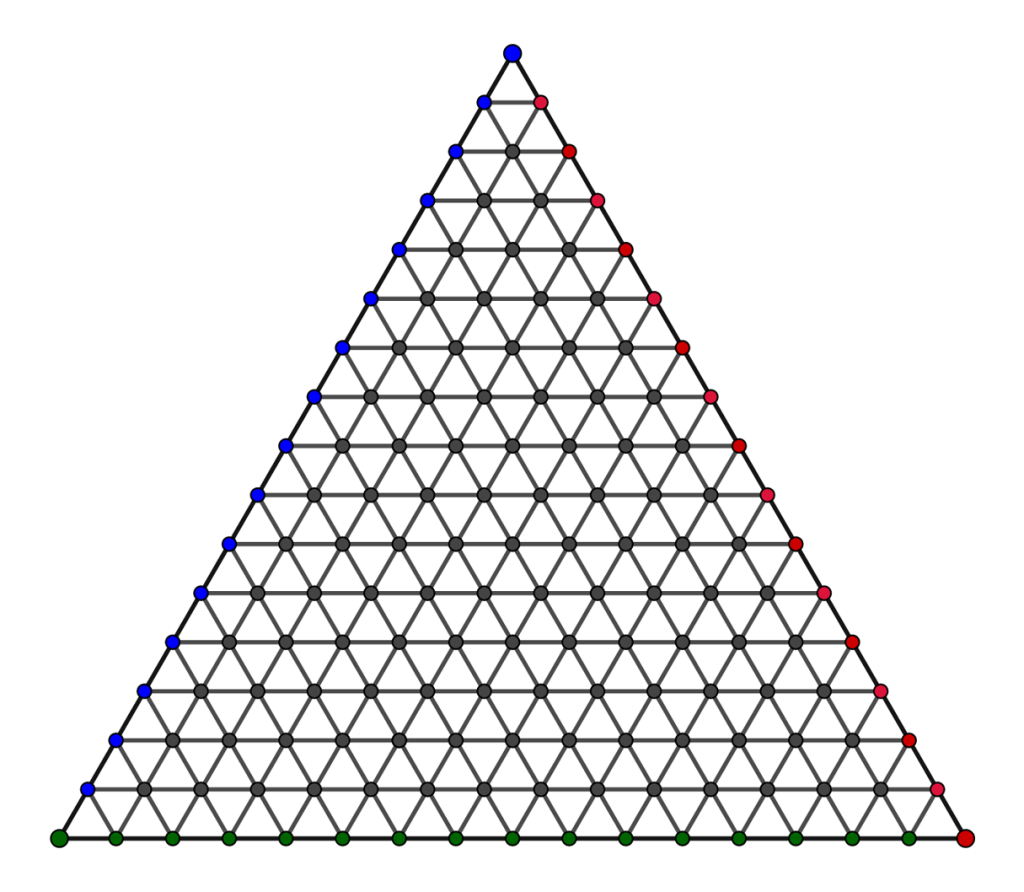
Two of the many possible boards for Triumph. Any size board can be used.
(The mathematically inclined may notice that a fractal known as Sierpinski’s triangle (opens new window) hides within the board.) As in the diagram, the vertices on the outer edges of this board are colored in a precise way: No color can be found along all three edges. This is the starting point of the game. Part of the beauty of Triumph is that the rules are simple: Two players compete, and each takes turns coloring an interior vertex. If at any point in the game, a player makes a small triangle with all three colors on its vertices, then that player “claims” that triangle. If playing on a sheet of paper, for example, a claimed triangle can be initialed with that player’s first initial. Play proceeds until all vertices are colored. Here is a game in progress:
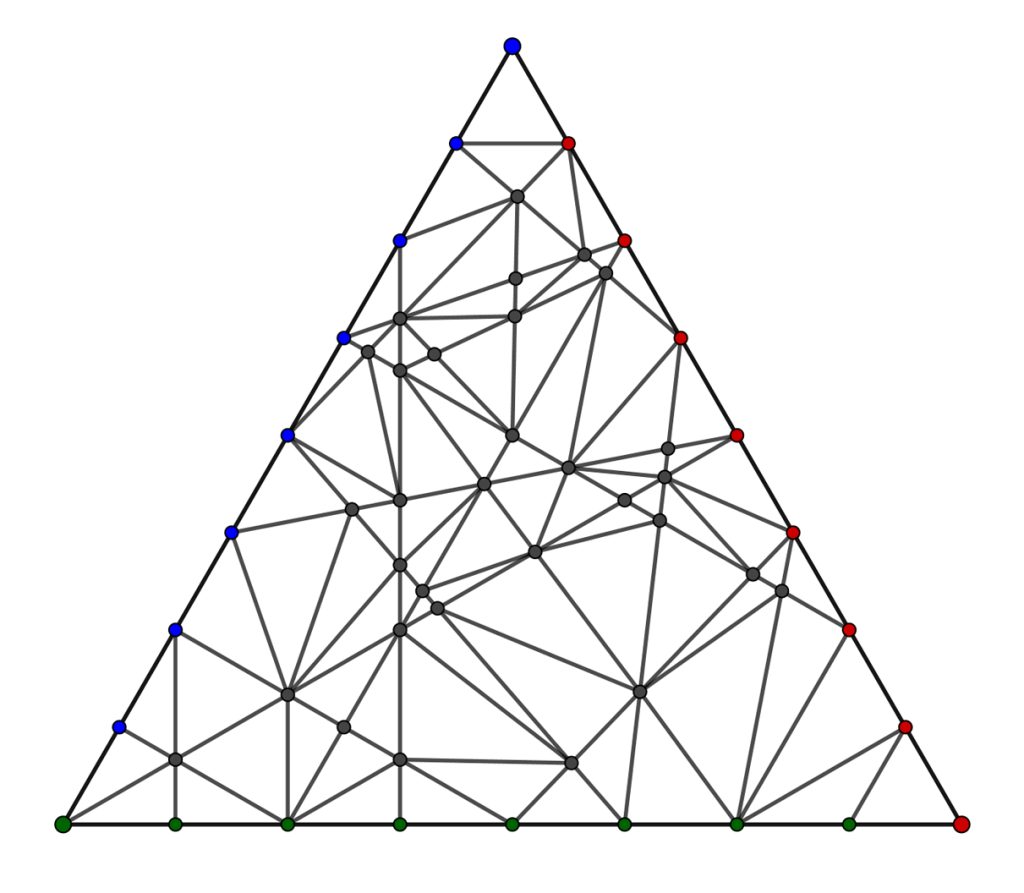
An incomplete game of Triumph. At the end of the game, there will be some unclaimed triangles.
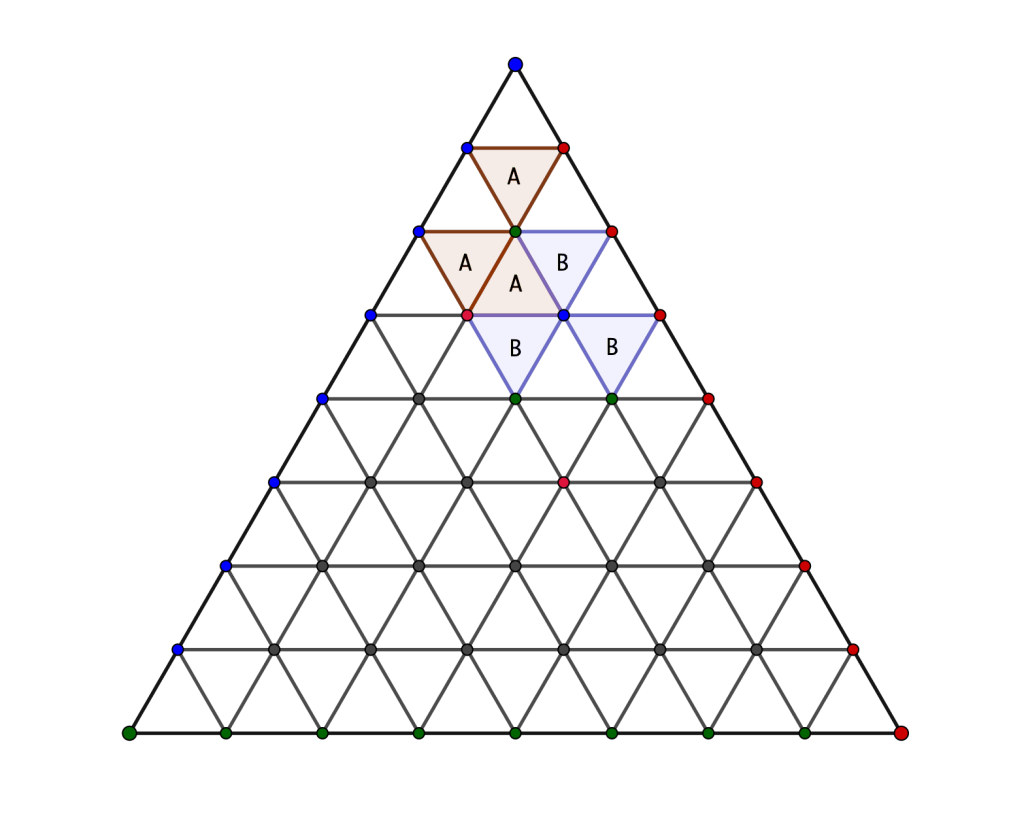
By some mathematics which we’ll now explain, the number of claimed triangles must be odd once the game is finished, which implies that this game always has a winner. Such games are called determined games in game theory. Triumph takes advantage of a well-known result in graph theory called Sperner’s Lemma (opens new window), which states that any coloring of the outer vertices of the simplex that has no color on all three outer sides must contain an odd number of small triangles which have all three colors on their vertices. Here are a few visual examples of alternative colorings from those given above:
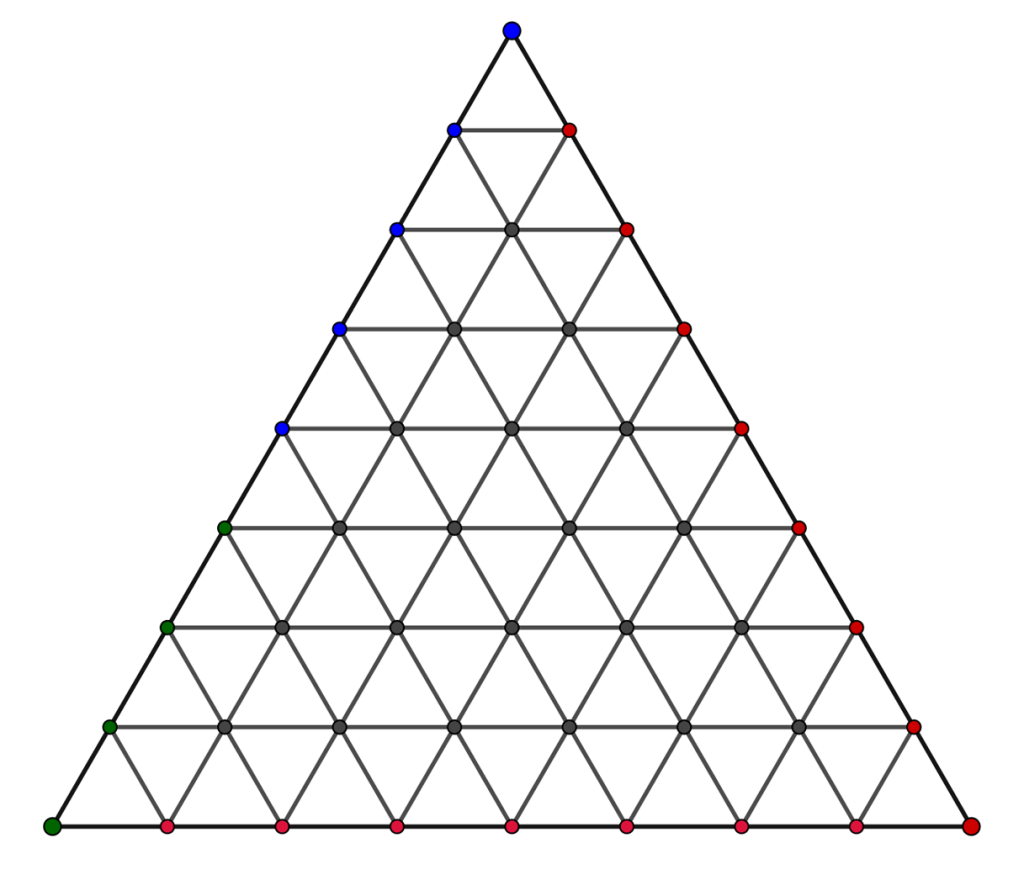
Two alternative valid colorings for a Triumph board.
If you’re feeling adventurous, Triumph can be played with any coloring of the outer vertices which satisfy the “no color on all sides” condition.
In mathematics, Sperner’s lemma underlies the Brouwer fixed point theorem in topology, the celebrated Nash equilibrium in game theory, the cut-and-choose method in fair division problems, Monsky’s theorem on partitions of a square into triangles of equal area, solutions to differential equations, the Jordan Curve theorem in topology, and much, much more. It is possible to state versions of Sperner’s lemma in higher dimensions, so Triumph can be played on a tetrahedron, too – with four colors and some creativity in physical construction!
Triangulations of 3-dimensional objects. Credit to Clément Jamin, Sylvain Pion and Monique Teillaud.
For the strategically inclined, try to play with a friend and see if you can find techniques that seem to succeed more often. Is there a best way to play Triumph? How does your answer to this depend on your opponent’s moves? We asked these questions at the Festival when playing Triumph with visitors of all ages, and despite the ease of play, optimal strategies were quite complex. From the teacher’s perspective, this makes for an excellent way to explore choice and geometric structure with students, especially because the initial board is simple for anyone to draw. Triumph is useful at all levels due to its close connections to higher mathematics.
More details on Triumph and other interesting new mathematical games will soon be posted online at http://edspace.american.edu/jward/ (opens new window)– check back later in summer 2019.
Jacob M. Ward is a Professorial Lecturer in Mathematics and Statistics at American University. A number theorist with special interests in finite fields (a general version of binary arithmetic (opens new window)) and geometry, his most recent work (opens new window) created the unit circle for finite fields and developed its structural theory. He is also interested in finite game design using objects like search trees, gerrymandered congressional districts, and social networks. He is one of the faculty Directors of the DC Math Circle (opens new window), where games with similar mathematical flavor are topics of exhilarating weekly activities!

